滑动窗口是面试中一大难点，幸运的是我们有模板

滑动窗口

Sliding Windows，是一类很看重细节的问题，题目通常为Medium或者hard

LC11.盛水最多的容器，

给你一个字符串 S、一个字符串 T，请在字符串 S 里面找出：包含 T 所有字符的最小子串。

示例：

输入: S = "ADOBECODEBANC", T = "ABC"
输出: "BANC"

如果 S 中不存这样的子串，则返回空字符串 ““。如果 S 中存在这样的子串，我们保证它是唯一的答案。

在滑动窗口中有两个指针，一个指针静止，而另一个指针保持移动。我们在s上滑动窗口，如果能够包含整个T（注意，T可能有重复字符），如果能收缩，我们就收缩窗口直到得到最小窗口。

fig1

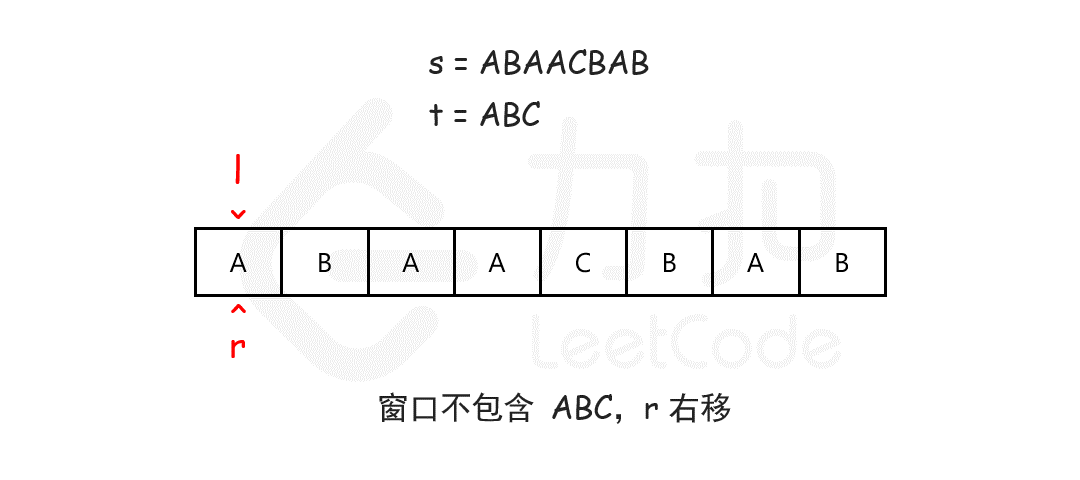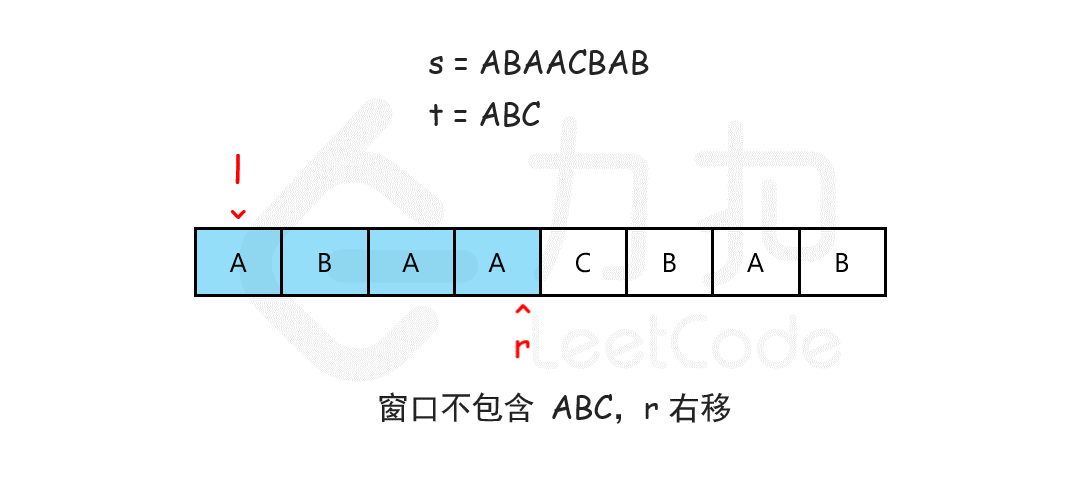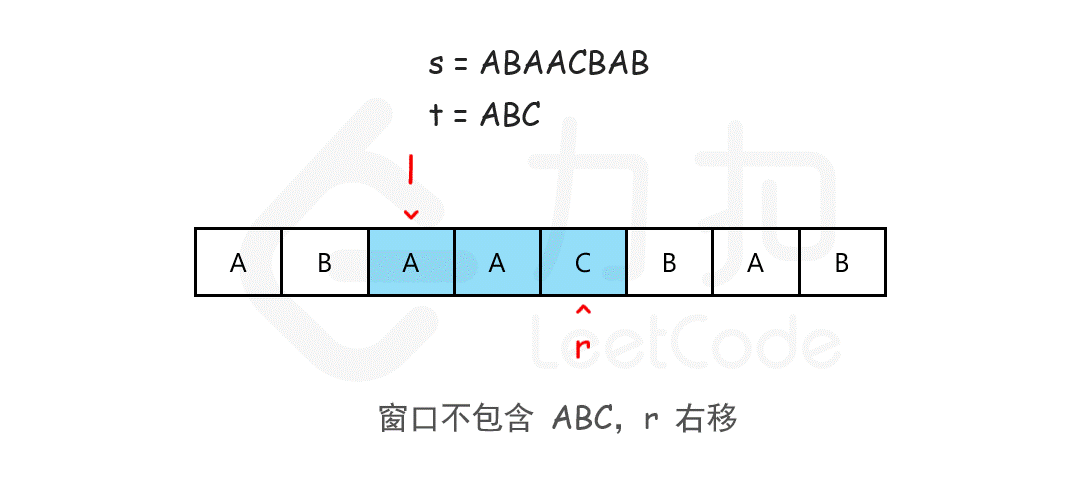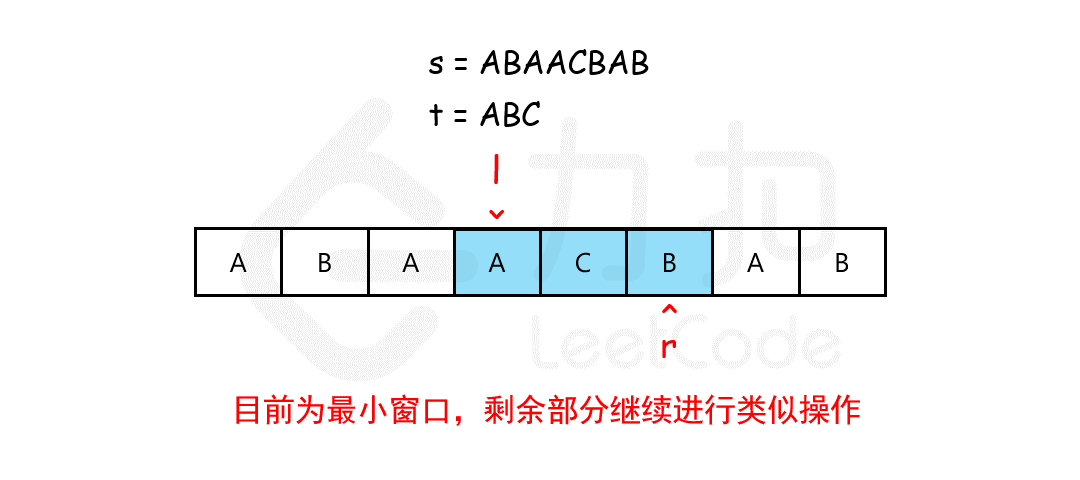
下面介绍一下滑动窗口法思路：

我们在字符串S中使用左右指针技巧，初始化left=right=0，把索引左闭右开区间[left,right)称为一个窗口。
我们先不断增加right指针扩大窗口，直到窗口中的字符串满足要求。
此时我们停止增加 right，转而不断增加left指针缩小窗口，直到窗口中的字符串不再满足要求。同时，每增加left，我们都要更新一轮结果。
重复2,3直到right到达字符串S的尽头。

滑动窗口的基本框架

int left = 0, right = 0;
while(right<s.size())
{
window.add(s[right])
right++
while(the window needs shrink)
{
window.pop(s[left])
left++
}
}

比较难的问题

LC.632最小区间

你有 k 个升序排列的整数数组。找到一个最小区间，使得 k 个列表中的每个列表至少有一个数包含在其中。

我们定义如果 b-a < d-c 或者在 b-a == d-c 时 a < c，则区间 [a,b] 比 [c,d] 小。

输入:[[4,10,15,24,26], [0,9,12,20], [5,18,22,30]]
输出: [20,24]
解释: 
列表 1：[4, 10, 15, 24, 26]，24 在区间 [20,24] 中。
列表 2：[0, 9, 12, 20]，20 在区间 [20,24] 中。
列表 3：[5, 18, 22, 30]，22 在区间 [20,24] 中。

注意:

给定的列表可能包含重复元素，所以在这里升序表示 >= 。
1 <= k <= 3500
-105 <= 元素的值 <= 105
对于使用Java的用户，请注意传入类型已修改为List<List>。重置代码模板后可以看到这项改动。

在讲这个方法之前我们先思考这样一个问题：有一个序列 $A = \{ a_1, a_2, \cdots, a_n \}$ 和一个序列 $B = \{b_1, b_2, \cdots, b_m\}$ ，请找出一个 B 中的一个最小的区间，使得在这个区间中 A 序列的每个数字至少出现一次，请注意 A 中的元素可能重复，也就是说如果 A 中有 p 个 u，那么你选择的这个区间中 u 的个数一定不少于 p。

回到这道题，我们发现这两道题的相似之处在于都要求我们找到某个符合条件的最小区间，我们可以借鉴「76. 最小覆盖子串」的做法：这里序列 $\{ 0, 1, \cdots , k - 1 \}$ 就是上面描述的 A 序列，即 k 个列表，我们需要在一个 B 序列当中找到一个区间，可以覆盖 A序列。这里的 B 序列是什么？我们可以用一个哈希映射来表示 B 序列—— B[i]表示 ii 在哪些列表当中出现过，这里哈希映射的键是一个整数，表示列表中的某个数值，哈希映射的值是一个数组，这个数组里的元素代表当前的键出现在哪些列表里。也许文字表述比较抽象，大家可以结合下面这个例子来理解。

如果列表集合为：

[-1, 2, 3]
[1]
[1, 2]
[1, 1, 3]

那么可以得到这样一个哈希映射

-1: [0]
[1, 2, 3, 3]
[0, 2]
[0, 3]

我们得到的这个哈希映射就是这里的 BB 序列。我们要做的就是在 B 序列上使用双指针维护一个滑动窗口，并用一个哈希表维护当前窗口中已经包含了哪些列表中的元素，记录它们的索引。遍历 B 序列的每一个元素：

指向窗口右边界的指针右移当且仅当每次遍历到新的元素，并将这个新的元素对应的值数组中的每一个数加入到哈希表中指向窗口左边界的指针右移当且仅当当前窗口内的元素包含 A中所有的元素，同时将原来左边界对应的值数组的元素们从哈希表中移除答案更新当且仅当当前窗口内的元素包含 A 中所有的元素。

个人理解是，这题也一样可以套用模板，need（即B）哈希表的键为nums中出现的所有数字，值为该数字所在的所有数组在nums中的序号。window为一个长度为n的数组，只有当前的区间覆盖了所有nums中子数组，才能进行窗口缩小操作。注意,这里的left和right分别是nums中所有数的最大值和最小值。


    vector<int> smallestRange(vector<vector<int>>& nums) {
    if(!nums.size()) return {};
    int n = nums.size();
    unordered_map<int, vector<int>> B;//B数组
    int xMin = INT32_MAX, xMax = INT32_MIN;//区间最大值和最小值
    //这里的need包含了nums中所有数及其所在列表序号的映射对
    for (int i = 0; i < nums.size();i++) 
    for (const auto &c:nums[i])
    {
        B[c].push_back(i);
        xMin = min(c,xMin);
        xMax = max(c,xMax);
    }// sort(need.begin(),need.end());
    
    int inside = 0; // 表示包含最小区间的数组的个数,等于n表示窗口可以开始缩小
    vector<int> freq(n);//A中每个子数组，被最小区间包含的次数
    int left = xMin, right = xMin-1;
    int ansL = INT32_MAX, ansR = 0; 
    int min_inter = INT32_MAX;
    while (right < xMax) {
        // 右移窗口
        right++;
        // 进行窗口内数据的一系列更新
        
        if(B.count(right))
        for(auto &c:B[right])
        {
            freq[c]++;
            if(freq[c]==1) inside++;
        }
        /*** debug 输出的位置 ***/
        printf("window: [%d, %d)\n", left, right);
        /********************/
        
        // 判断左侧窗口是否要收缩
        while (inside==n) {
            // 进行窗口内数据的一系列更新
            if(right-left+1 < min_inter||(right-left+1 == min_inter&&left<ansL))
            {
                min_inter = right-left+1;
                ansL = left;
                ansR = right;
            }

            if(B.count(left))
            for(auto &c:B[left])
            {
                freq[c]--;
                if(freq[c]==0) inside--;
            }

            // 左移窗口，注意要放在后面，否则无法更新freq中左区间
            left++;
            
        }
    
    }
    return {ansL,ansR};
    
    }

未完待续。。

滑动窗口

LC.632最小区间

FEATURED TAGS

FRIENDS