解空间极大问题通用策略
比如全排列问题,组合问题等。以78.子集为例。
- 全排列
- 组合
- 子集 ,每个元素可能存在或者不存在
要确保结果完整且不重复,有三种策略:
- 递归
- 回溯
- 字典
递归
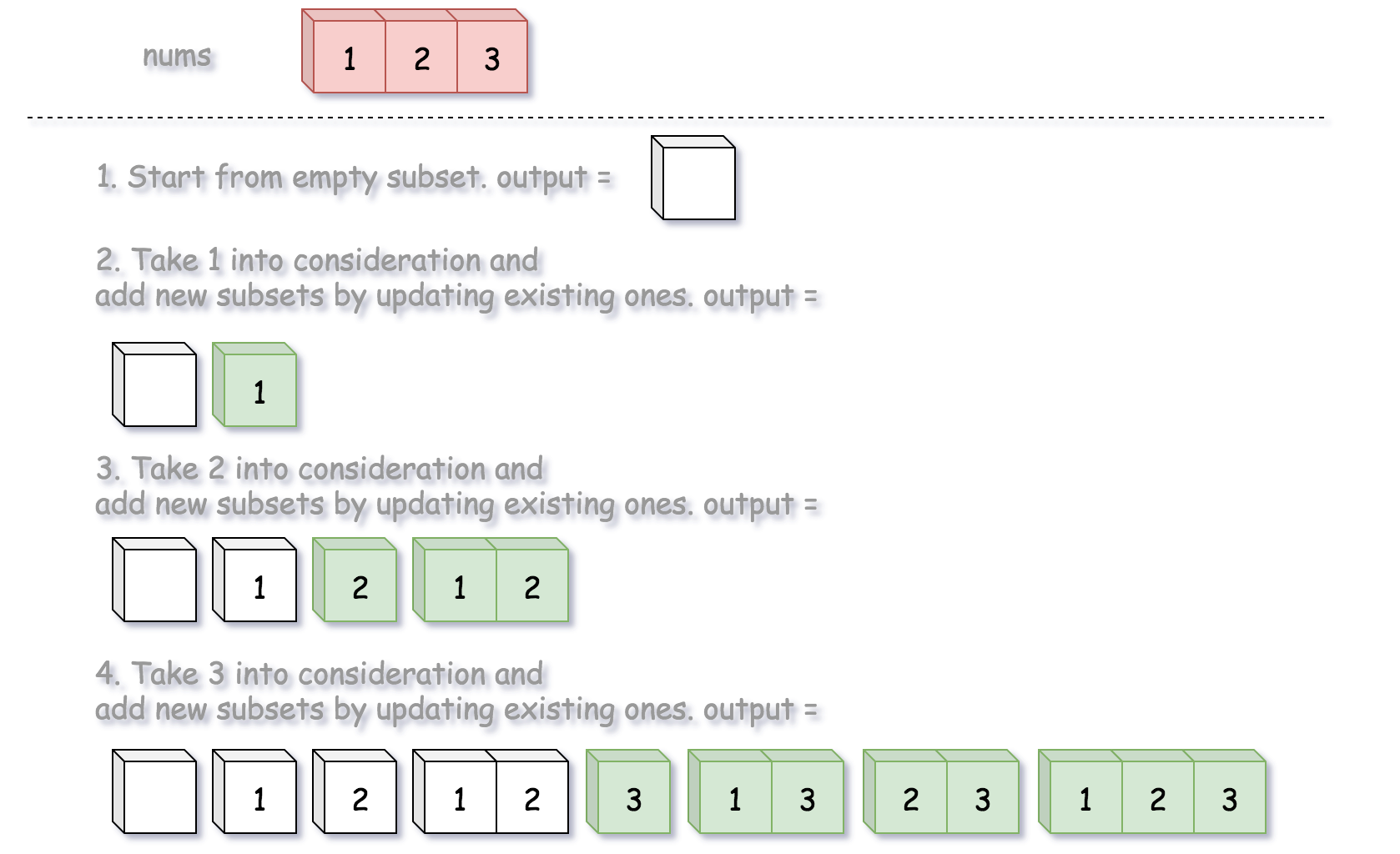
递归不一定是递归函数,而是逐层次的把nums下一个数与前面的数融合起来。
比如:
vector<vector<int>> subsets(vector<int>& nums) {
if(!nums.size()) return ;
res.push_back({});
for(auto &c:nums)
{
auto _res = res;
for(auto &k :_res)
{
k.push_back(c);
res.push_back(k);
}
}
return res;
}
时间复杂度:,生成所有子集,并复制到输出结果中。
空间复杂度:,这是子集的数量。
对于给定的任意元素,它在子集中有两种情况,存在或者不存在(对应二进制中的 0 和 1)。因此,N个数字共有 个子集。
回溯
回溯法(探索与回溯法)是一种选优搜索法,又称为试探法,按选优条件向前搜索,以达到目标。但当探索到某一步时,发现原先选择并不优或达不到目标,就退回一步重新选择,这种走不通就退回再走的技术为回溯法,而满足回溯条件的某个状态的点称为“回溯点”。
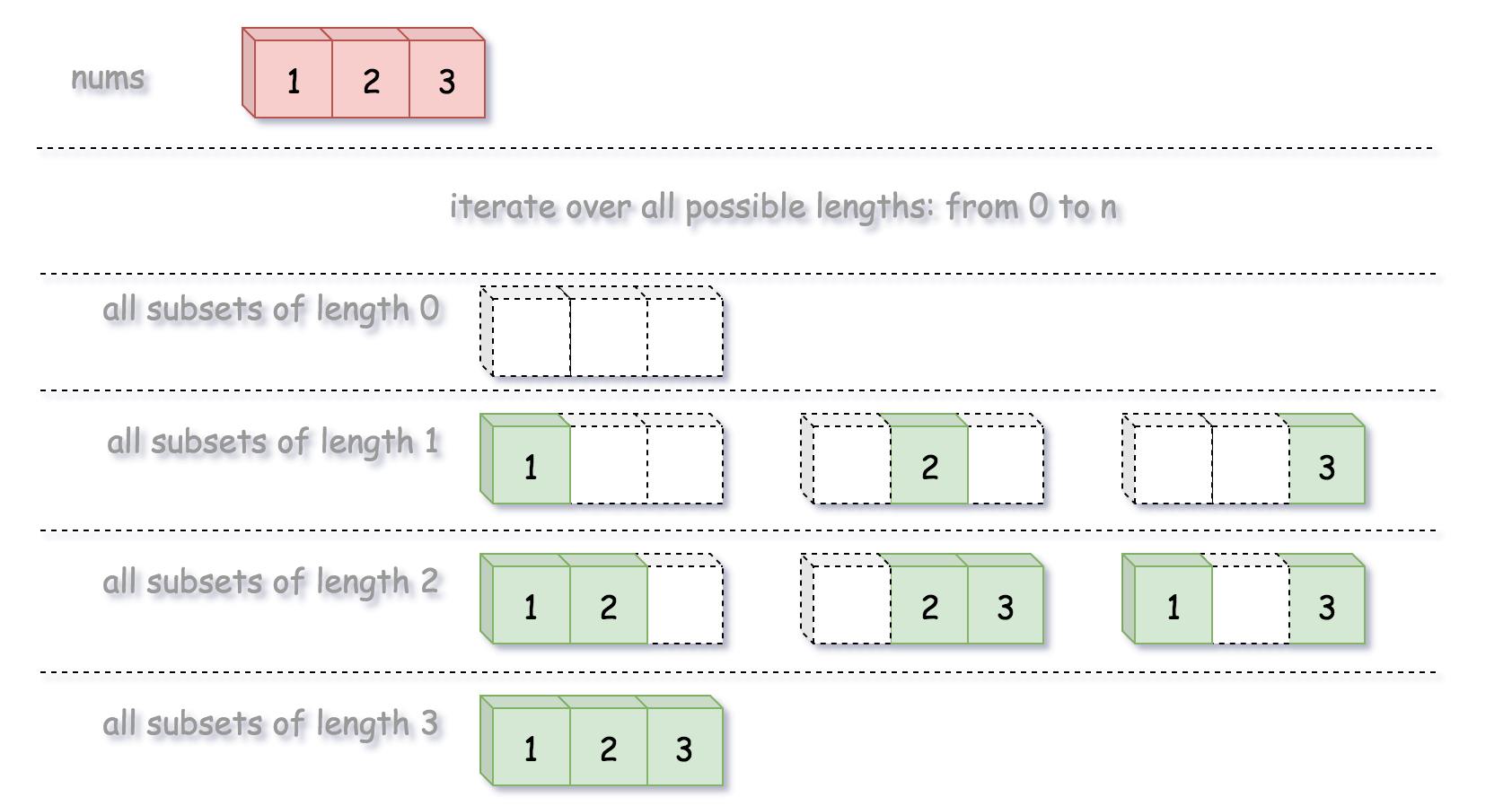
以该题为例,比如我们要在[1,2,3]中找到所有子集,思路是这样的:
定义一个回溯方法 backtrack(first, curr),第一个参数为索引 first,第二个参数为当前子集 curr。
-
如果当前子集构造完成,将它添加到输出集合中。
-
否则,从 first 到 n 遍历索引 i。
- 将整数 nums[i] 添加到当前子集 curr。
- 继续向子集中添加整数:backtrack(i + 1, curr)。
- 从 curr 中删除 nums[i] 进行回溯。
![]()
int n;
vector<int> nums;
void backtrack(int first, vector<int> &curr)
{
if(first>=n) return;
for (int i = first; i < n; i++)
{
curr.push_back(nums[i]);
res.push_back(curr);
backtrack(i+1, curr);
curr.pop_back();
}
}
vector<vector<int>> subsets(vector<int>& nums)
{//回溯法
if(!nums.size()) return ;
this->n = nums.size();
this->nums = nums;
vector<int> curr;
backtrack(0, curr);
res.push_back({});
return res;
}
时间复杂度:,生成所有子集,并复制到输出结果中。
空间复杂度:,这是子集的数量。
对于给定的任意元素,它在子集中有两种情况,存在或者不存在(对应二进制中的 0 和 1)。因此,N个数字共有 个子集。
字典
该方法思路来自于Donald E. Knuth
将每个子集映射到长度为n的掩码中,其中第i位掩码nums[i]为1,表示第i个元素在子集中, 如果第i位掩码nums[i]位0,表明第i位元素不在子集中。
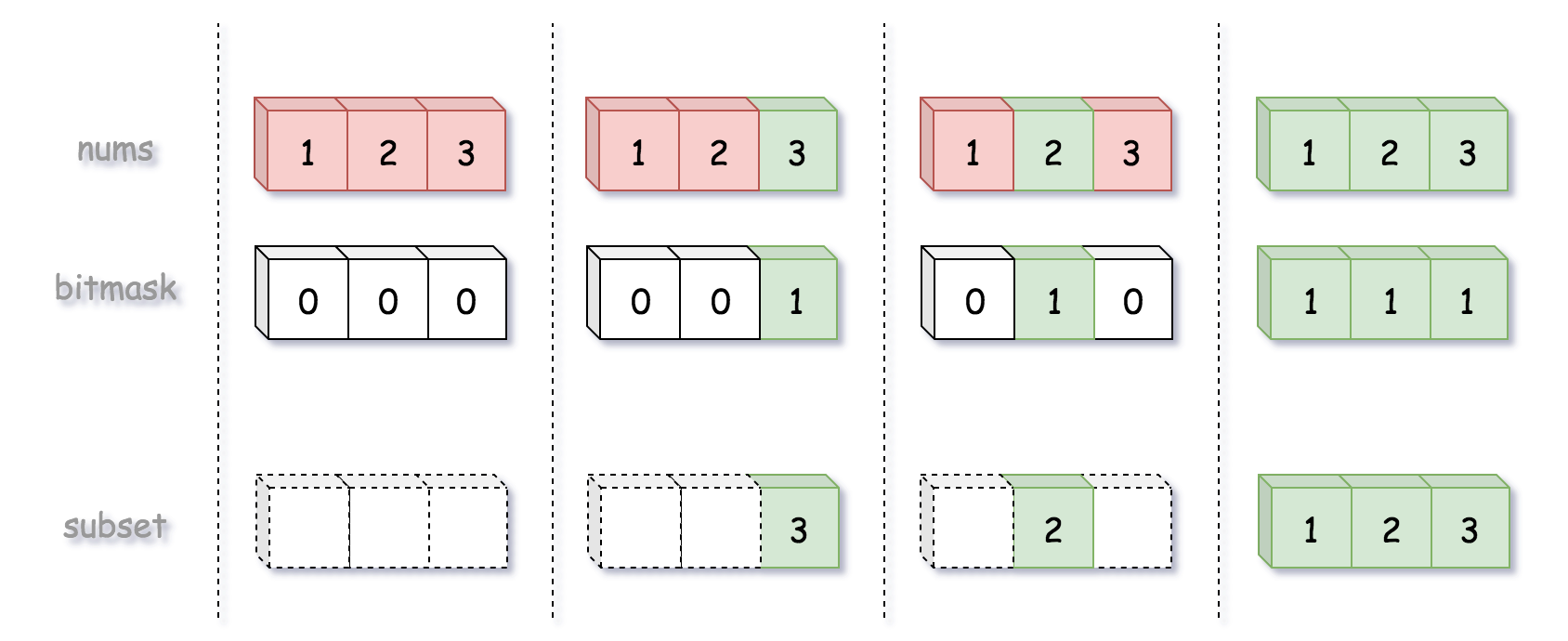
乍看起来生成二进制数很简单,但如何处理左边填充 0 是一个问题。因为必须生成固定长度的位掩码:例如 001,而不是 1。因此可以使用一些位操作技巧:
nth_bit = 1 << n
for i in range(2**n):
# generate bitmask, from 0..00 to 1..11
bitmask = bin(i | nth_bit)[3:]
class Solution:
def subsets(self, nums: List[int]) -> List[List[int]]:
n = len(nums)
output = []
for i in range(2**n, 2**(n + 1)):
# generate bitmask, from 0..00 to 1..11
bitmask = bin(i)[3:]
# append subset corresponding to that bitmask
output.append([nums[j] for j in range(n) if bitmask[j] == '1'])
return output
时间复杂度:,生成所有子集,并复制到输出结果中。
空间复杂度:,这是子集的数量。
对于给定的任意元素,它在子集中有两种情况,存在或者不存在(对应二进制中的 0 和 1)。因此,N个数字共有 个子集。
一些子母问题(数字重复与不重复)
46 全排列
数字不重复,求全排列,回溯法
class Solution {
public:
void backtrack(vector<vector<int>>& res, vector<int>& output, int first, int len){
// 所有数都填完了
if (first == len) {
res.emplace_back(output);
return;
}
for (int i = first; i < len; ++i) {
// 动态维护数组
swap(output[i], output[first]);
// 继续递归填下一个数
backtrack(res, output, first + 1, len);
// 撤销操作
swap(output[i], output[first]);
}
}
vector<vector<int>> permute(vector<int>& nums) {
vector<vector<int> > res;
backtrack(res, nums, 0, (int)nums.size());
return res;
}
};
47 全排列2
数字重复,求全排列【此时一定要用hash表】
vector<vector<int>> res;
vector<int> nums;
vector<int> arr;
unordered_map<int,int> dict;
void dfs(int n)
{
if(n==0)
{
res.push_back(arr);
return;
}
for(auto &c:dict)
{
if(c.second>0)
{
arr.push_back(c.first);
c.second--;
dfs(n-1);
c.second++;
arr.pop_back();
}
}
}
vector<vector<int>> permuteUnique(vector<int>& nums) {
if(!nums.size()) return ;
this->nums = nums;
for(auto &c:nums)
dict[c]++;
dfs(nums.size());
return res;
}
78 子集(上面作为例子讲了)
90 子集2
求包含重复元素的所有子集
class Solution {
public:
vector<pair<int, int>> data;
vector<vector<int>> res;
int n;
vector<int> tmp;
void dfs(int i) {
if (i == n) {
res.push_back(tmp);
return ;
}
dfs(i + 1);
//i是从n-1开始
for (int j = 0; j < data[i].second; j ++) {
tmp.push_back(data[i].first);
dfs(i + 1);
}
for (int j = 0; j < data[i].second; j ++) tmp.pop_back();
return ;
}
vector<vector<int>> subsetsWithDup(vector<int>& nums) {
unordered_map<int, int> mp;//统计nums每个数字的个数
for (auto x : nums) {
mp[x] ++;
}
for (auto x : mp) {
data.push_back(x);//相当于把哈希表存到数组
}
n = data.size();
dfs(0);
return res;
}
};