一提到红黑树,你应该是这样想的。。。
上一期我们详细分析了AVL树,相信你已经对二叉平衡树有了非常棒的理解。这一期我们开始介绍红黑树,红黑树在网上有很多资源,但是讲的不严谨,也不全面。笔者初学时也浪费了许多时间,因此我将非常细致的讲解,将自己踩过的坑晒出来,保证你能看懂。
红黑树和AVL树的区别是:AVL树是严格平衡的二叉树,红黑树是弱平衡的二叉树。和红黑树相比,AVL树是严格的平衡二叉树,平衡条件必须满足(所有节点的左右子树高度差不超过1)。通过对任何一条从根到叶子的路径上各个节点着色的方式的限制,红黑树确保没有一条路径会比其它路径长出两倍,因此相同节点数的前提下,AVL树的高度往往低于红黑树。AVL树根据节点的平衡因子进行调整,而红黑树是根据颜色进行调整。大致地说,红黑树理解上较容易,而实现起来,需要注意的细节要更多(比如说考虑叔叔节点)。推荐大佬博客:比较两者不同。
为什么要学二叉树呢?(斜体表示你问了一个很棒的问题):
- 红黑树的结点增删改查效率非常优良,都为log(n) , 应用方面:1. Linux内核进程调度由红黑树管理进程控制块。 2. Epoll用红黑树管理事件块。 3. nginx服务器用红黑树管理定时器。 4. C++ STL中的map和set的底层实现为红黑树。 5. Java中的TreeMap和TreeSet由红黑树实现。 6. Java8开始,HashMap中,当一个桶的链表长度超过8,则会改用红黑树。
下面我们看一下红黑树的性质:
1. 每个节点要么是黑色,要么是红色
2. 根节点一定为黑色
3. 每一个空节点(null / NIL)都是黑色(注意空节点不等于根节点)
4.一旦一个节点为黑色,它的孩子一定为黑色,也就是说,不可能有父子节点同时为红色。
5. 对每个节点而言,从每个黑色节点到叶子节点的节点数量相同。
因此我们需要对树可视化函数稍作修改,对每个节点上色。对turtle,使用 t.fillcolor来设置填充颜色,t.begin_fill和t.end_fill来实现开始填充和结束填充,非常方便。

笔者得到的树如上图所示,是不是很美观呢?但是光美观是不够的,我们还得实现背后的逻辑,而这也是最酷炫的部分。我保证,如果你能亲手成就一个红黑树,能让你“快乐”很长时间。
和AVL树类似,红黑树只需要在节点类加入颜色属性即可。为了后期代码方便,我们实现两个函数,一个是获取当前节点的叔叔节点get_uncle,另一个是获取兄弟节点get_brother
def get_uncle(self):
if not self.parent or not self.parent.parent: return None
if self.parent.parent.hasBothChildren():
if self.parent.isLeftChild():
return self.parent.parent.right_child
else:
return self.parent.parent.left_child
def get_brother(self):
if not self.parent : return None
if self.parent.hasBothChildren():
if self.isLeftChild():
return self.parent.right_child
else:
return self.parent.left_child
好了,我们依旧从插入和删除来讨论算法
1. Put方法实现
我们和AVL树类比,其实就是将平衡因子改变的过程变为更新颜色的过程而已,为此我们需要实现一个函数renew_color。需要注意的是每当创建一个新的叶子节点时候,它都应该是红色的。理由很简单,红色在父结点(如果存在)为黑色结点时,红黑树的黑色平衡没被破坏,不需要做自平衡操作。但如果插入结点是黑色,那么插入位置所在的子树黑色结点总是多1,必须做自平衡。
旋转过程在我上篇的AVL树博客中已经介绍(需要的读者自行食用),红黑树中的旋转也完全相同。
我们来作一些简单的设定。

在这幅图中,当前节点为B,那么其兄弟节点为E,其父节点为D,它的叔节点为A,祖父节点为C。
我们由浅入深 循序渐进来化解这个问题:
(1)若树为空树,那么直接添加一个节点作为根节点,且为黑色(事实上,根节点一定为黑色)。
(2)插入节点的key已经存在,那么我们只需要将节点的val更新成新的val即可。
(3)插入节点的父节点为黑节点,那么插入新节点不会影响树的平衡,直接插入即可。
(4)插入节点 的父节点为红色节点,插入节点也为红色,明显不平衡。且父节点肯定不是根节点,我们需要详细的讨论这种情况:
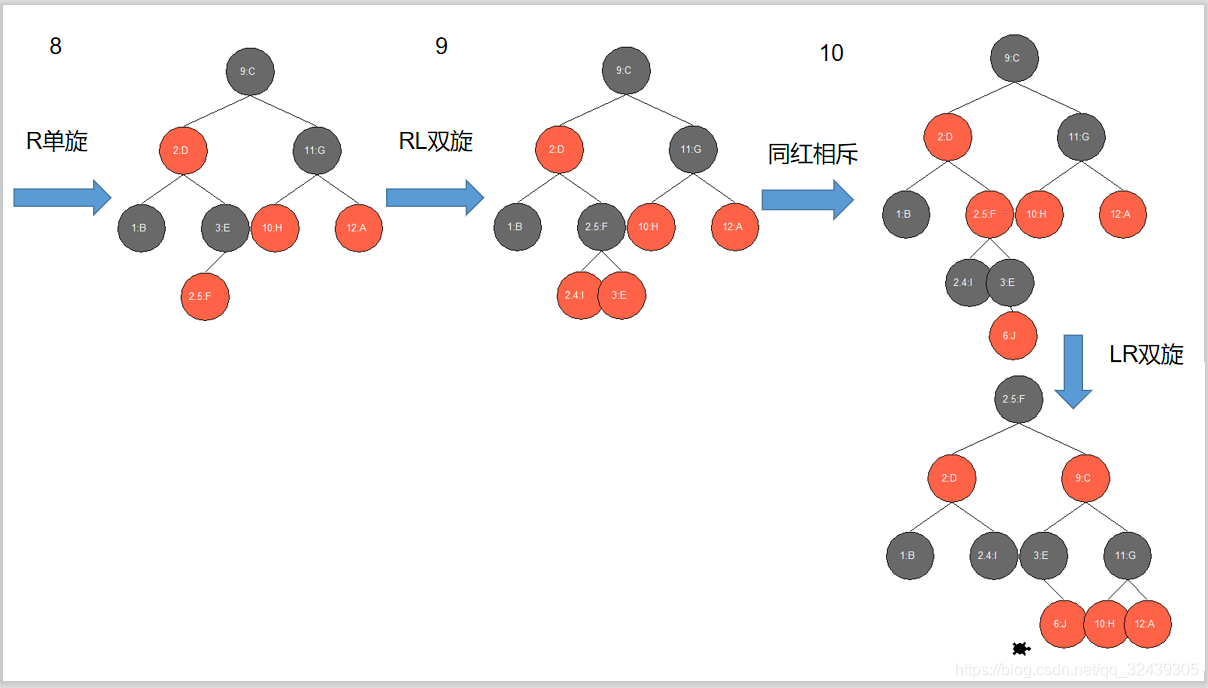
1. 叔叔节点存在,并且叔叔节点为红色:

当前节点为B,此时父节点的左子树和右子树肯定是不平衡的。给你10s请你想一想,如何满足性质5?
一种直观的想法是将父节点D\C全部变为黑色,然后将当前节点B和其兄弟节点I
变为红色。

然后我们需要考虑当前节点的祖父节点的颜色F。如果它不是根节点,我们需要将其颜色变为红色,然后将祖父节点变为当前节点继续向上平衡。注意,只有所有子树都平衡的情况下,整个树才是平衡的。简言之,红黑树平衡是至下而上的,而AVL树是自上而下的。
2. 插入节点的父节点是左子节点
这时候我们看当前节点是左子节点还是右子节点:
右子节点:我们对祖父节点A进行LR双旋,祖父节点变为红色,父节点变为黑色 。

左子节点:对祖父节点A进行R单旋,同时将父节点颜色设为黑色,叔叔节点设为红色

3. 插入节点的父节点是右子节点
与左子节点情况刚好相反,故不再演示,但是调试时候注意考虑这种情况。
OK,上面便是插入操作,我们来测试一下,数据为data = {12:’A’,1:’B’,9:’C’,2:’D’,3:’E’,2.5:’F’,11:’G’,10:’H’,2.4:’I’,6:’J’}
2. Del方法实现
现在我们考虑更复杂的删除情况。你需要一杯咖啡,因为接下来内容会比较多和干燥。但是我保证你看完之后会很有启发。
现在我们写一个def __delitem__函数,这样我们就能使用del 关键字删除特定key了。我们先简单回顾一下,
(1)如果待删除的结点是叶子结点,则直接删除即可。
(2)如果待删除的结点只有一个孩子,则设定currNode.parent.left_child = currNode.left_child或者currNode.parent.right_child = currNode.right_child,替换节点为其独子。
(3)如果待删除的结点有两个孩子,则可以找它的后继,将值覆盖过来,之后情况转变成删除前驱或者后继结点,回到(1)和 (2)。
删除的含义在于,删的不是节点本身,而是它的“替身”。(你可以想象成JOJO里的替身使者:->)
下面是 正片 即在删除之前,我们必须更新颜色和进行旋转,这些在函数update_del_color()中体现:
先考虑几个边值条件:
1. 树为空,直接返回None即可;
2. 利用get_node函数找到需要删除的节点,如果没找到,直接返回None。
3. 如果替换节点是红色的,将其改为黑色,因为删除红色节点不会影响平衡
所谓的再平衡无异乎是找兄弟或者父母去“借”,是不是很形象呢{坏笑}: 我们可以将当前节点分为左子节点和右子节点两种情况,它们是完全对称的,
- 先考虑左子节点情况:
假设实际被删除节点为C,
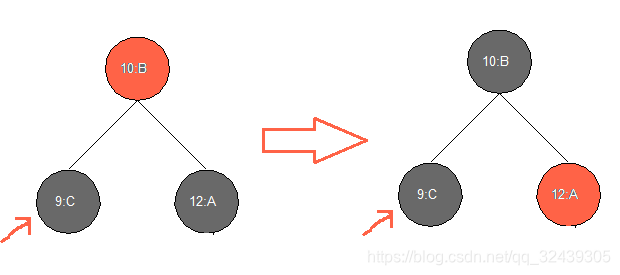
(a)父节点为红色,且兄弟节点没有子节点
我们将父节点变为黑色,同时将兄弟节点变为红色(兄弟节点一定没有子节点)。下面这个图可以直观展现这点:
(b)父节点为黑色,且兄弟节点没有子节点
我们将兄弟节点颜色改为红色,之后再对父节点执行update_del_color进行递归。

(c)兄弟节点左子节点存在,且为红色节点,右节点随意
那么这个时候我们需要考虑父节点B的颜色,因为兄弟左子节点D为红色,我们可以把它借出去,涂成父节点的颜色,再将父节点颜色设为黑色。之后对父节点B进行RL双旋,但是不要改变节点颜色,只有在插入时才改变节点颜色。

这里白色表示颜色不确定。
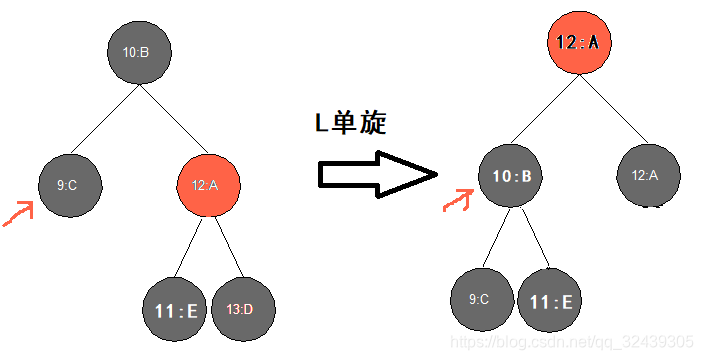
(d)兄弟节点右子节点存在,且为红色节点,左子节点为黑色
兄弟变为父节点颜色,同时父节点变为黑色,而且右侄子变为黑色。再对父节点进行左旋。

(e)兄弟节点有两个儿子,且兄弟为红色节点
我们直接对父节点左旋,这就变成上面兄弟为黑色情况,再调用update_del_color对父节点进行递归:
- 当前节点为右子节点,刚好相反,故不再赘述
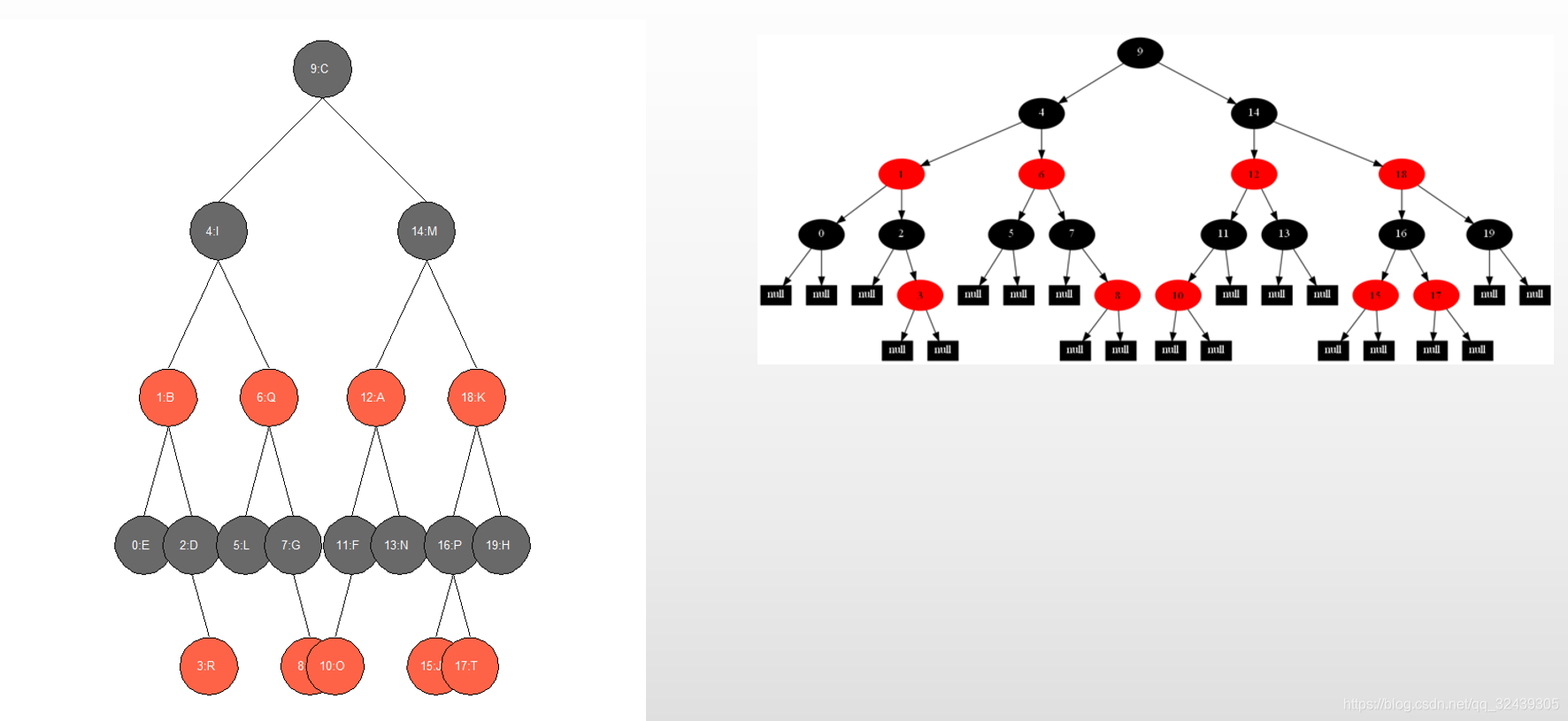
下面我们将完整的过程展现出来,根据July的博客https://blog.csdn.net/v_july_v/article/details/6284050。
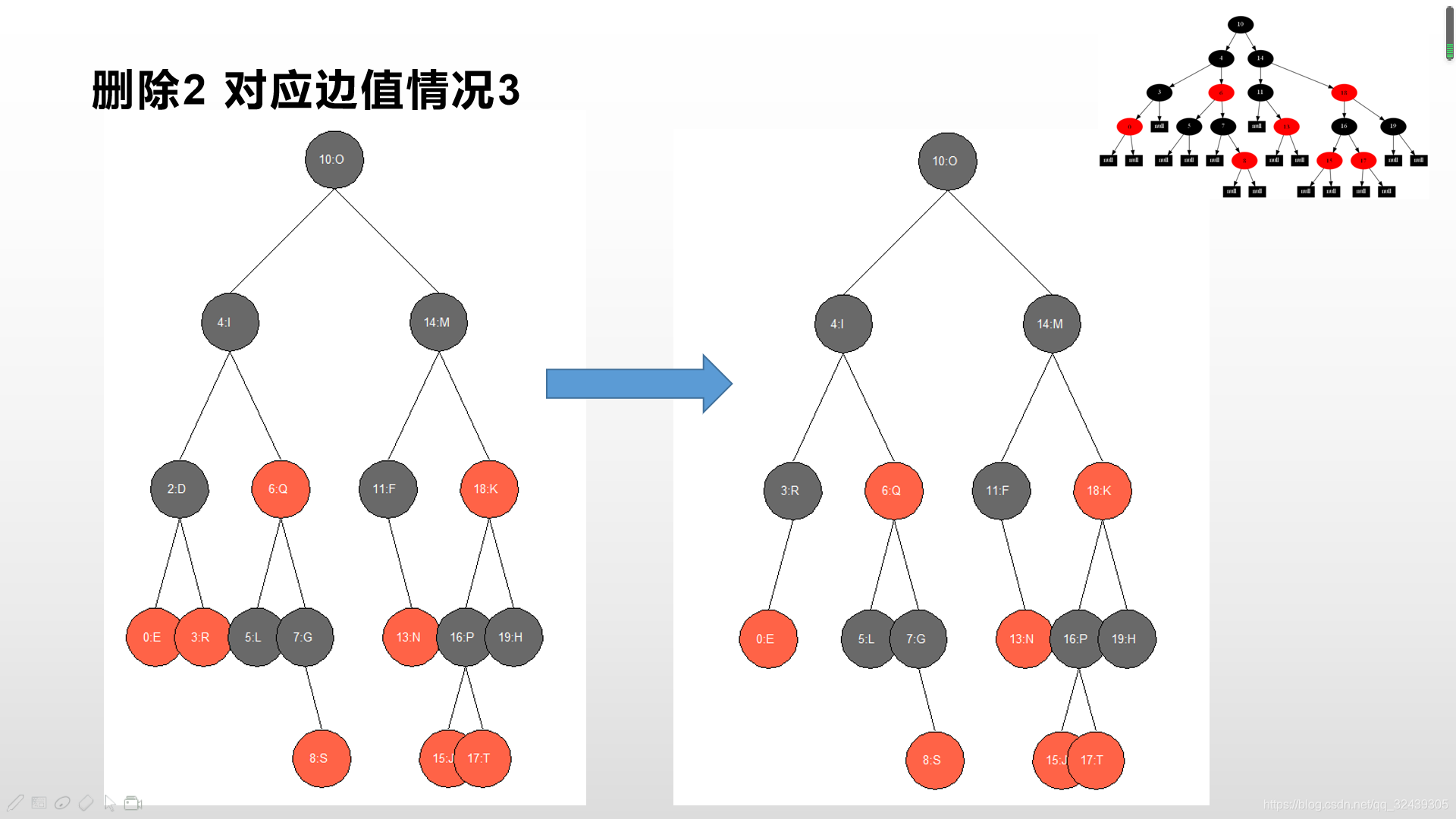
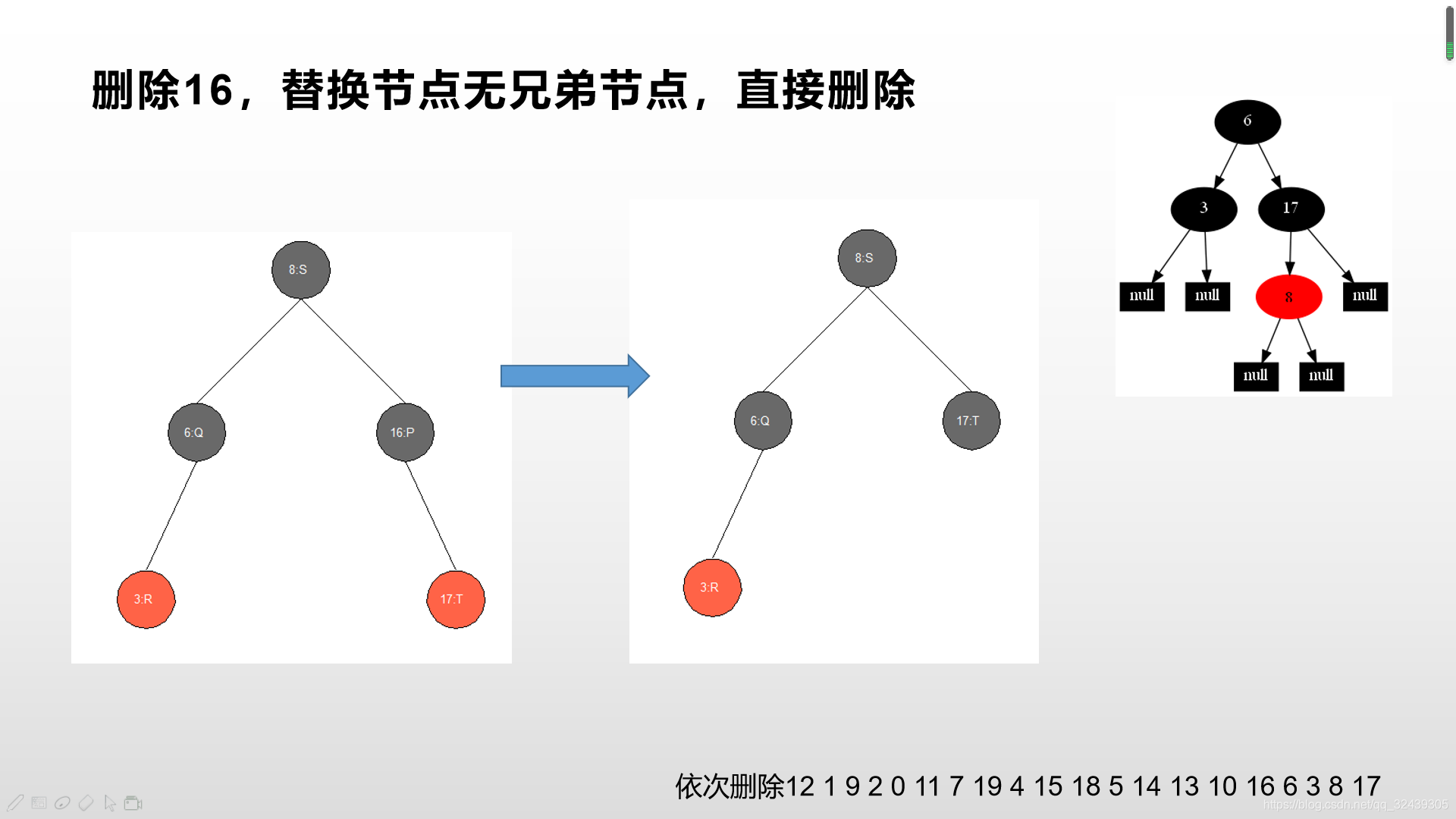
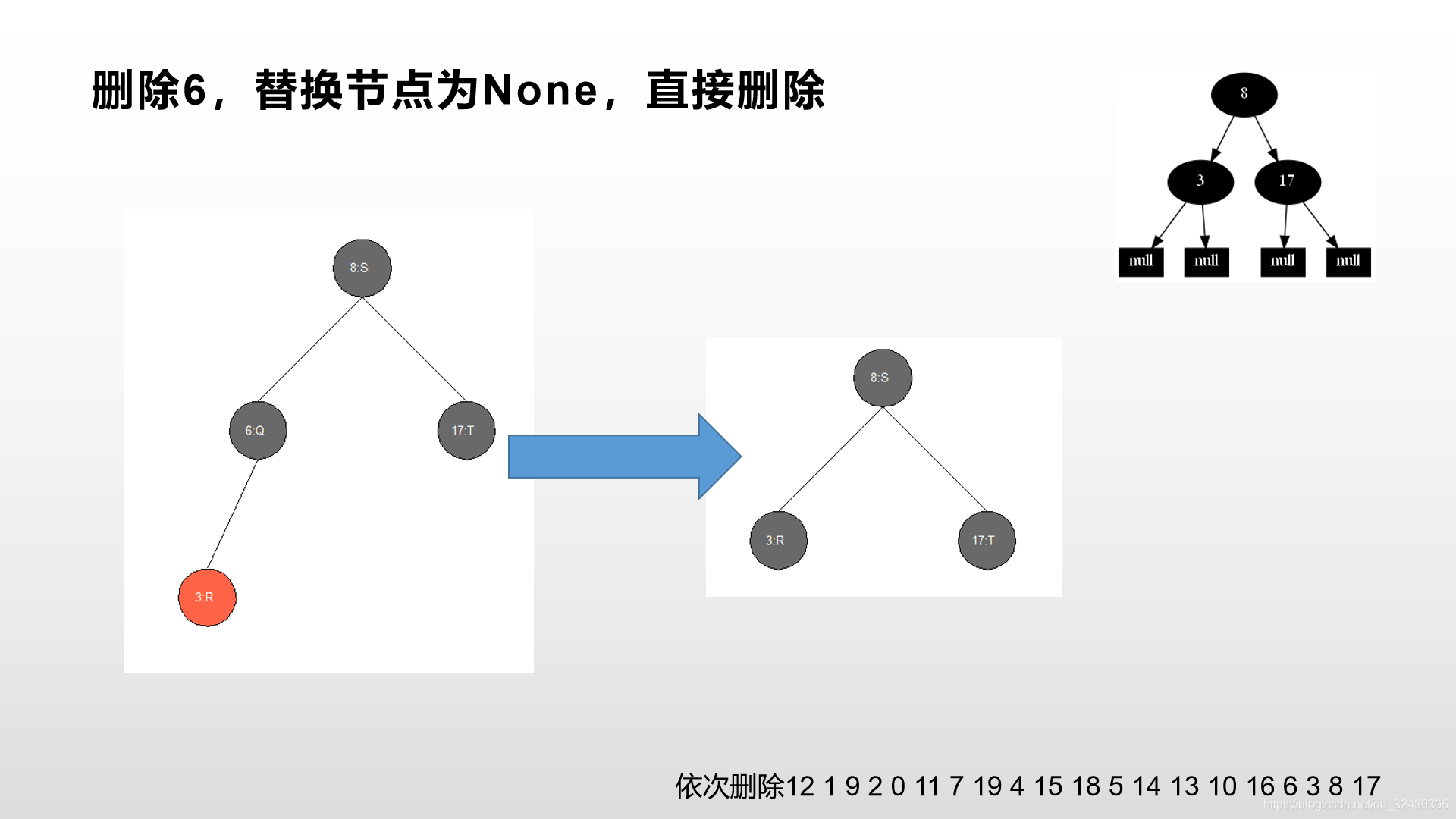
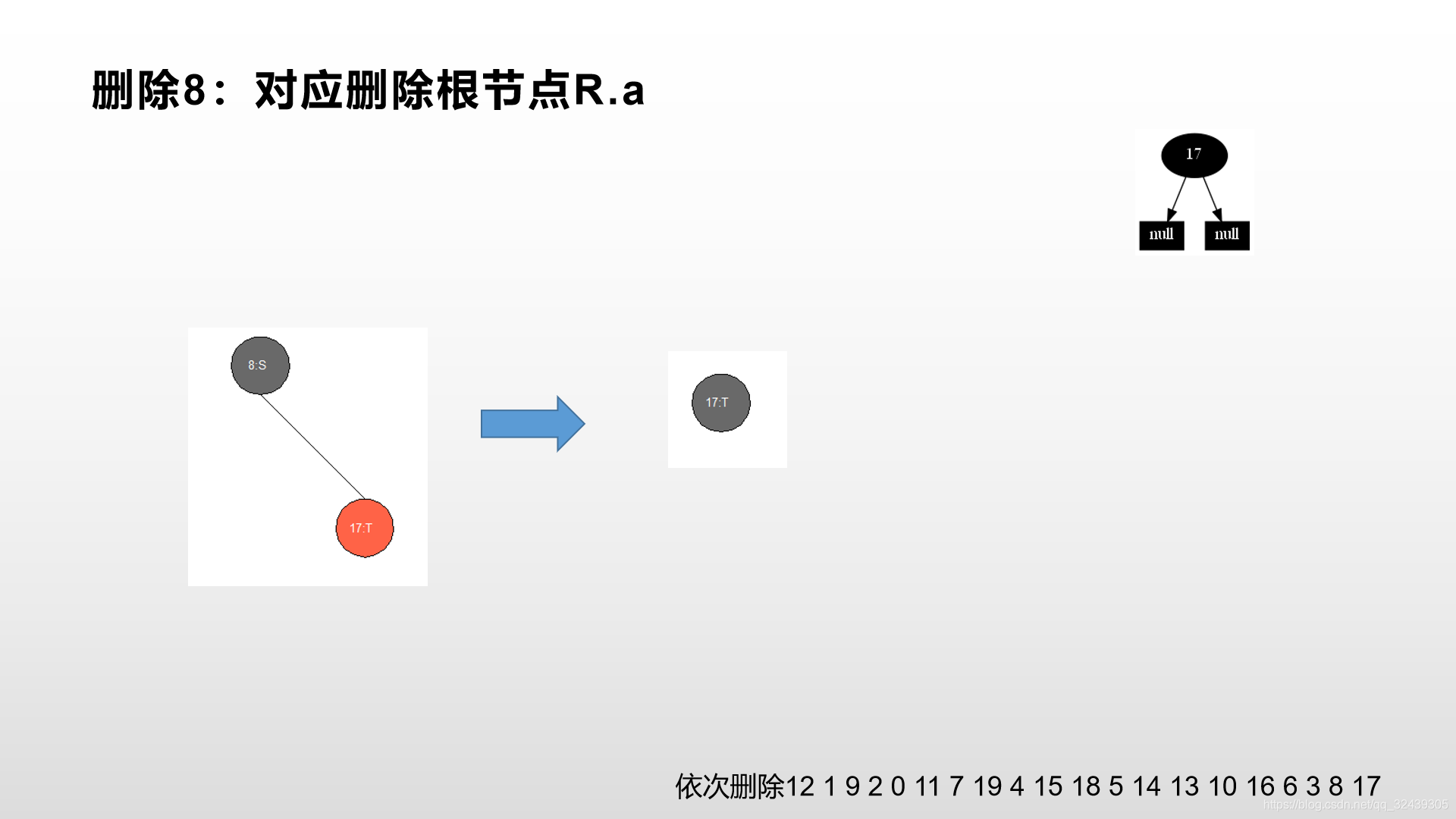
依次删除12 1 9 2 0 11 7 19 4 15 18 5 14 13 10 16 6 3 8 17。 大家可以作一个对比,如果你有任何问题,请立刻在下方留言!笔者不胜感激。
- 完整的红黑树















希望本文对你有帮助,
源代码在这里!
码字不易,希望大家多多转发,多点赞!邮箱durant2019@sina.com